Você já ouviu falar que juros compostos são como uma “bola de neve”? Eles fazem seu dinheiro crescer de forma exponencial, e quando você adiciona aportes regulares a essa equação, o resultado pode ser ainda mais impressionante! Mas como calcular tudo isso? Calma, não precisa ser um gênio da matemática para entender. Neste post, vamos descomplicar o cálculo de juros compostos com aportes, para que você possa planejar seus investimentos e alcançar seus objetivos financeiros com mais segurança.
O que são Juros Compostos?
Antes de falarmos sobre os aportes, vamos relembrar o conceito de juros compostos. Diferentemente dos juros simples, que incidem sempre sobre o valor inicial, os juros compostos são calculados sobre o valor inicial mais os juros já acumulados. Ou seja, seus juros geram mais juros, criando um efeito “bola de neve” ao longo do tempo.
E os Aportes? Onde Entram Nessa História?
Os aportes são as contribuições regulares que você faz ao seu investimento, como depósitos mensais, por exemplo. Ao adicionar aportes, você está turbinando ainda mais o poder dos juros compostos. Imagine que você está cultivando uma planta: os juros compostos são a força que faz ela crescer, e os aportes são a água e o adubo que a mantêm forte e aceleram esse crescimento.
A Fórmula (Descomplicada) dos Juros Compostos Com Aportes
A fórmula exata para calcular juros compostos com aportes pode parecer um pouco assustadora à primeira vista. Mas, não se preocupe, vamos simplificar! Em vez de nos aprofundarmos em equações complexas, vamos apresentar uma forma mais didática de entender o processo:
- Calculando o Montante do Período Anterior: Comece com o valor inicial do seu investimento (seu “ponto de partida”). Aplique a taxa de juros do período (geralmente mensal ou anual). Isso te dará o montante que você terá após o primeiro período.
- Adicionando o Aporte: Agora, adicione o valor do seu aporte regular a esse montante.
- Repetindo o Processo: O resultado desse passo é o novo montante sobre o qual você calculará os juros do próximo período. E você repete o processo, calculando os juros e adicionando o aporte, até o final do período desejado.
Exemplo Prático: Vamos Colocar em Números
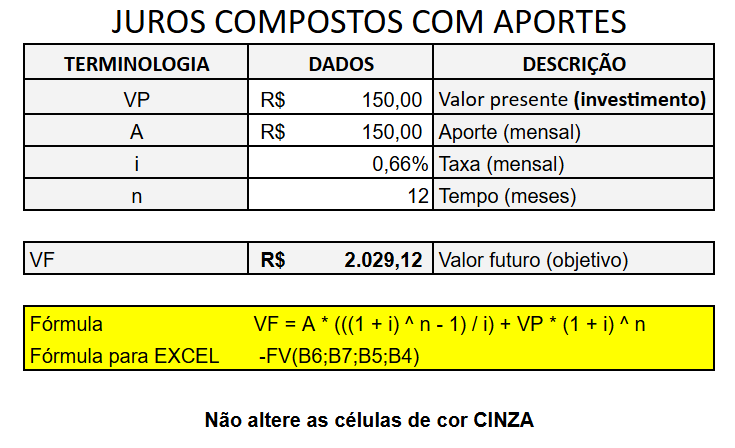
Valor inicial R$ 150,00 , aporte mensal de R$ 150,00 com uma taxa de 0,66% ao mês em 12 meses você terá um valor de: R$ 2029,12.
Você pode utilizar nossa calculadora abaixo.
Imagine que você está construindo uma montanha de dinheiro, tijolo por tijolo:
Essa fórmula calcula o tamanho final dessa montanha (o montante total do seu investimento) quando você:
- Começa com um valor inicial: É o primeiro tijolo da sua montanha.
- Faz depósitos regulares: Você adiciona novos tijolos todo mês (ou período).
- Tem um crescimento contínuo: A cada período, os juros fazem seus tijolos crescerem, e esse crescimento também se junta à montanha.
A Fórmula em Partes:
A fórmula é dividida em duas partes principais:
- Aporte Mensal + Juros:
- aporte mensal * (((1 + taxa) ^ tempo - 1) / taxa): Esta parte da fórmula calcula o valor total de todos os seus depósitos ao longo do tempo, considerando o poder dos juros compostos sobre cada depósito.
- Pense nisso como a "pilha de tijolos" que você está construindo a cada período. Cada tijolo não só se adiciona à pilha, mas também cresce com os juros.
- 1 + taxa: Representa o crescimento do dinheiro a cada período (ex: 1.05 seria um crescimento de 5% por período)
- (1 + taxa) ^ tempo: Eleva esse crescimento ao número de períodos, que é o seu tempo de investimento, para levar em conta o efeito composto.
- (1 + taxa) ^ tempo - 1: Remove o valor inicial do seu crescimento para chegar no crescimento dos aportes em si.
- / taxa: Divide pela sua taxa de juros para que possa se adequar à quantidade de tempo, quanto tempo você está investindo.
- Valor Inicial + Juros:
- valor inicial * (1 + taxa) ^ tempo: Esta parte calcula o crescimento do seu tijolo inicial, ao longo do tempo.
- Pense nisso como o primeiro tijolo da sua montanha, que também vai crescer com os juros.
Juntando tudo
No final, a fórmula junta essas duas partes, o crescimento dos aportes (os tijolos novos) com o crescimento do valor inicial (o primeiro tijolo) para calcular o tamanho final da sua montanha de dinheiro.
Conclusão
O cálculo de juros compostos com aportes pode parecer complicado no início, mas com um pouco de conhecimento e a ajuda de ferramentas, você pode dominar essa ferramenta poderosa para alcançar seus objetivos financeiros. Lembre-se: quanto mais cedo você começar e quanto mais consistente você for com seus aportes, maiores serão os resultados. Então, que tal começar agora mesmo a planejar seu futuro financeiro?
Bônus
E você, já utilizou o poder dos juros compostos com aportes? Compartilhe sua experiência nos comentários!
